是什么

Thrift是一个跨语言的RPC框架，它可以通过Thrift的IDL（接口定义语言）来描述接口函数及数据类型，编译后可以自动生成服务端的框架代码。

RPC框架可以分为服务治理和跨语言调用两大类型。前者一般和语言耦合度高，且提供了丰富的功能（负载均衡，服务注册与发现等），比如Java的Dubbo框架。而后者主要解决不同语言的服务间的调用问题，没有太多花哨的功能，比如gRPC，Thrift。

优缺点

优点是可以跨语言使用，性能优秀，自动生成服务端代码，使用起来简单方便。

缺点是没有动态特性。

原理

Thrift是一种C/S的架构体系.在最上层是用户自行实现的业务逻辑代码。下层是由Thrift编译器自动生成的代码，主要用于结构化数据的解析，发送和接收。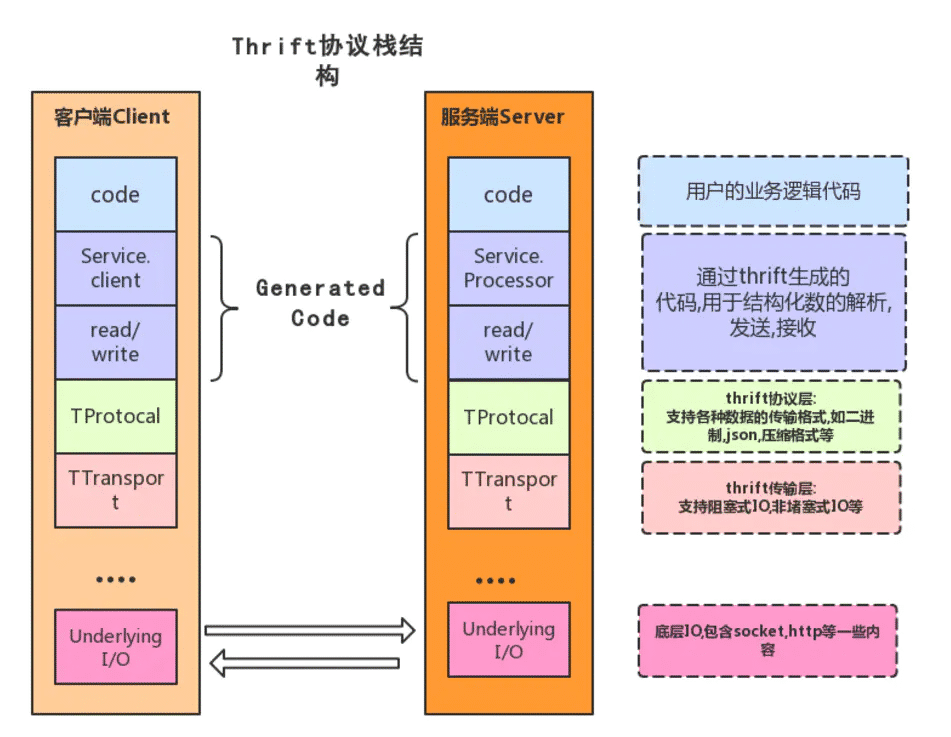

Transport:

为从网络进行读写提供了简单的抽象。负责以字节流方式接收和发送消息体，不关注是什么数据类型。底层IO负责实际的数据传输，包括socket、文件和压缩数据流等。它解耦了上层部分（如序列化）与数据的传输。

Protocol：

TProtocol是用于数据类型解析的，即序列化和反序列化，将结构化数据转化为字节流给TTransport进行传输。

Processor:

从输入流中读入数据，然后委托给处理代码进行处理（自己编写），最后写到输出流中。输入、输出流由下层的Protocal对象提供，接口非常简单：

1
2
3

interface TProcessor {
    bool process(TProtocol in, TProtocol out) throws TException
}

Server：

整合了上面所有的功能：

• Create a transport
• Create input/output protocols for the transport
• Create a processor based on the input/output protocols
• Wait for incoming connections and hand them off to the processor

实例

我们使用Thrift实现一个匹配系统，客户端调用远程服务器将用户两两间进行匹配，比如玩各种1V1游戏时，将段位相似的玩家匹配到一起。客户端使用Python，服务端使用Java。

源码在 https://github.com/xiaoxiaokun/ThriftDemo。

定义服务器接口

使用thrift定义的类型写一个thrift文件，再使用 thrift -r --gen <language> <thrift file> 自动生成客户端和服务端代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

namespace java match

struct Player
{
    1: i32 id,
    2: string name,
    3: i32 score
}

service Match {

  /**
   * A method definition looks like C code. It has a return type, arguments,
   * and optionally a list of exceptions that it may throw. Note that argument
   * lists and exception lists are specified using the exact same syntax as
   * field lists in struct or exception definitions.
   */

   i32 add(1:i32 id, 2:string name, 3:i32 score),

   i32 remove(1:i32 id, 2:string name)

}

使用命令生成的源码主要有两个文件，一个文件封装thrift中定义的接口方法，一个文件封装定义的类型。我们只需要在服务端实现该接口，在客户端调用该接口即可。

客户端

使用Python编写，用上述命令生成Python源码，主要得到 ttype.py 和 Math.py 两个文件。我们新建一个client.py文件来编写客户端的操作，先获取一个连接服务器的客户端对象，该对象中有在Thrift中写的接口方法，再直接调用即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

from pydoc import cli
from sys import stdin

from match import Match
from match.ttypes import *

from thrift import Thrift
from thrift.transport import TSocket
from thrift.transport import TTransport
from thrift.protocol import TBinaryProtocol

def operate(op, id, username, score):
    # Make socket
    transport = TSocket.TSocket('localhost', 9090)

    # Buffering is critical. Raw sockets are very slow
    transport = TTransport.TBufferedTransport(transport)

    # Wrap in a protocol
    protocol = TBinaryProtocol.TBinaryProtocol(transport)

    # Create a client to use the protocol encoder
    client = Match.Client(protocol)

    # Connect!
    transport.open()

    print(op)
    if op == 'add':
        client.add(id, username, score)
    elif op == 'remove':
        client.remove(id, username)

    # Close!
    transport.close()

def main():
    while True:
        line = stdin.readline()
        if not line:
            break
        line = line.strip()
        if not line:
            continue
        op, id, username, score = line.split()
        operate(op, int(id), username, int(score))

if __name__ == '__main__':
    main()

服务端

用Java编写，生成源码后得到 Match.java 和 Player.java 文件，和生成的Python源码类似。

Match主要提供了Iface的接口，我们只要实现其中的add和remove方法即可，其余的创建Transport、创建Protocol、创建Server只需要调用Thrift提供的现成的实现类就好，而且Thrift对每一层的接口都提供了多种实现，用户可以根据需要选择合适的实现类，比如Server层提供了单线程和多线程实现，处理器也提供了同步和异步的实现。

创建一个 MatchServerHandle 类来实现接口中的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

public class MatchServerHandle implements Match.Iface {
	@Override
	public int add(int id, String name, int score) {
		log.info("add...");
		MatchServer.Task task = new MatchServer.Task();
		task.player = new Player(id, name, score);
		task.opType = "add";
		synchronized (MatchServer.taskQueue) {
			MatchServer.taskQueue.add(task);
			MatchServer.taskQueue.notify();
		}
		return 0;
	}

	@Override
	public int remove(int id, String name) {
		log.info("remove...");
		MatchServer.Task task = new MatchServer.Task();
		task.player = new Player(id, name);
		task.opType = "remove";
		synchronized (MatchServer.taskQueue) {
			MatchServer.taskQueue.add(task);
			MatchServer.taskQueue.notify();
		}
		return 0;
	}
}

创建一个服务端的启动类，负责监听客户端请求，并创建添加、移除玩家的任务：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

public class MatchServer {
	private static MatchServerHandle handler;
	private static Match.Processor<MatchServerHandle> processor;
	private static MatchPool pool;

	static class Task {
		Player player;
		String opType;
	}

	static final Queue<Task> taskQueue = new ConcurrentLinkedQueue<>();

	public static void main(String[] args) throws TException {
		try {
			handler = new MatchServerHandle();
			processor = new Match.Processor<>(handler);
			pool = new MatchPool();

			TServerTransport serverTransport = new TServerSocket(9090);
			TServer server = new TSimpleServer(new TThreadPoolServer.Args(serverTransport).processor(processor));
			log.info("Match Server Starting...");

			Runnable createTask = MatchServer::createTask;
			new Thread(createTask, "crtTaskTread").start();

			server.serve();

		} catch (Exception x) {
			x.printStackTrace();
		}
	}

	/**
	 * 消费任务，进行添加、删除、匹配用户等操作
	 *
	 */
	private static void createTask() {
		while (true) {
			synchronized (taskQueue) {
				if (taskQueue.isEmpty()) {
					try {
						taskQueue.wait();
					} catch (InterruptedException e) {
						e.printStackTrace();
						return;
					}
				} else {
					// 创建add任务或remove任务
					Task t = taskQueue.poll();
					if ("add".equals(t.opType)) {
						pool.add(t.player);
					} else if ("remove".equals(t.opType)) {
						pool.remove(t.player);
					}
				}
				pool.match();
			}
		}
	}
}

还需要一个类负责处理任务，进行玩家间的匹配：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

public class MatchPool {
	TreeSet<Player> players = new TreeSet<>(Comparator.comparingInt(Player::getScore));

	public void add(Player player) {
		log.info("pool add player...");
		players.add(player);
	}

	public void remove(Player player) {
		log.info("pool remove player...");
		players.removeIf(p -> p.id == player.id);
	}

	public void match() {
		if (players.size() < 2) return;

		Player player1 = players.pollFirst();
		Player player2 = players.pollFirst();
		assert player1 != null;
		assert player2 != null;
		System.out.println("match " + player1.name + " and " + player2.name);
	}
}

这样就基本完成了，同时启动客户端和远处的服务端，在Python客户端中输入，远程的Java服务进行处理后返回响应。

5844、数组元素的最小非零乘积

给你一个正整数 p 。你有一个下标从 1 开始的数组 nums ，这个数组包含范围 [1, 2p - 1] 内所有整数的二进制形式（两端都 包含）。你可以进行以下操作任意次：从 nums 中选择两个元素 x 和 y  。
选择 x 中的一位与 y 对应位置的位交换。对应位置指的是两个整数 相同位置 的二进制位。比方说，如果 x = 1101 且 y = 0011 ，交换右边数起第 2 位后，我们得到 x = 1111 和 y = 0001 。请你算出进行以上操作 任意次 以后，nums 能得到的 最小非零 乘积。将乘积对 109 + 7 取余 后返回。注意：答案应为取余 之前 的最小值。

其实很快就能找到规律，但是这题问题就在于，求解过程中数字溢出，需要在每一处可能溢出的地方进行取余操作，同时配合记忆化递归进行快速幂求解。

下面是最终的代码，可以看到在很多处都进行了取余操作，因为求2^60级别的乘法中稍稍不注意就会Long型溢出了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
    public int minNonZeroProduct(int p) {
        // int的最大值是 2^31 - 1
        if (p == 1) return 1;
        long r = (long)Math.pow(2, p) - 1;
        
        long res = r % mod;    //取余
        res *= getPow(r - 1, r / 2);
        res %= mod;    //取余
        return (int)res;
    }
    
    long mod = 1000000007;
    HashMap<Long, Long> map = new HashMap<>();
    public long getPow(long num, long multi) {
        if (multi == 1) return num;
        if (map.containsKey(multi)) return map.get(multi);
        
        long res = getPow(num, multi / 2) % mod;   //取余
        res *= getPow(num, multi / 2) % mod;    //取余
        res %= mod;    //取余

        if (multi % 2 == 1) {
            res *= num % mod;     //取余
        }

        res %= mod;    //取余
        // System.out.println(res);
        map.put(multi, res);
        return res;
    }
}

还有一个问题在于：

long r = (int)Math.pow(2, p) - 1; 这句当p等于31时，按理说2 ^ 31转化为int时会溢出，结果应该是 -2147483648 - 1 = 2147483647，但是结果却是2147483646；当我在本地IDE进行(int)Math.pow(2, 31) 这个运算时，得到的结果也是2147483647，这就有点匪夷所思了。

初步排除了无符号的原因，因为如果是无符号，那最大值应该是2 ^ 32 - 1，那么Math.pow(2, 31) 应该得到的是2147483648。

想想这可能是JDK内部实现时进行的什么改变，下面是Java官方文档对于类型转换的解释：

Narrowing Primitive Conversion

22 specific conversions on primitive types are called the narrowing primitive conversions:

• short to byte or char
• char to byte or short
• int to byte, short, or char
• long to byte, short, char, or int
• float to byte, short, char, int, or long
• double to byte, short, char, int, long, or float

A narrowing primitive conversion may lose information about the overall magnitude of a numeric value and may also lose precision and range.

A narrowing primitive conversion from double to float is governed by the IEEE 754 rounding rules (§4.2.4). This conversion can lose precision, but also lose range, resulting in a float zero from a nonzero double and a float infinity from a finite double. A double NaN is converted to a float NaN and a double infinity is converted to the same-signed float infinity.

A narrowing conversion of a signed integer to an integral type T simply discards all but the n lowest order bits, where n is the number of bits used to represent type T. In addition to a possible loss of information about the magnitude of the numeric value, this may cause the sign of the resulting value to differ from the sign of the input value.

A narrowing conversion of a char to an integral type T likewise simply discards all but the n lowest order bits, where n is the number of bits used to represent type T. In addition to a possible loss of information about the magnitude of the numeric value, this may cause the resulting value to be a negative number, even though chars represent 16-bit unsigned integer values.

A narrowing conversion of a floating-point number to an integral type T takes two steps:

1. In the first step, the floating-point number is converted either to a long, if T is long, or to an int, if T is byte, short, char, or int, as follows:
   1. If the floating-point number is NaN (§4.2.3), the result of the first step of the conversion is an int or long 0.
   2. Otherwise, if the floating-point number is not an infinity, the floating-point value is rounded to an integer value V, rounding toward zero using IEEE 754 round-toward-zero mode (§4.2.3). Then there are two cases:
      1. If T is long, and this integer value can be represented as a long, then the result of the first step is the long value V.
      2. Otherwise, if this integer value can be represented as an int, then the result of the first step is the int value V.
   3. Otherwise, one of the following two cases must be true:
      1. The value must be too small (a negative value of large magnitude or negative infinity), and the result of the first step is the smallest representable value of type int or long.
      2. The value must be too large (a positive value of large magnitude or positive infinity), and the result of the first step is the largest representable value of type int or long.
2. In the second step:
   ◦ If T is int or long, the result of the conversion is the result of the first step.
   ◦ If T is byte, char, or short, the result of the conversion is the result of a narrowing conversion to type T (§5.1.3) of the result of the first step.

加粗的地方就是上面这种情况，从double转为int型中的第3中情况，当浮点数的值是转为后的数据类型的infinity时，如果超过负极值，就转为MIN_VALUE，如果超过正极值，就转为MAX_VALUE;

所以并不是所有的情况都会溢出。

还是挺常见的问题，感觉属于动态规划里的内容，但这部分东西也不少，而且很有规律，所以单独作为一篇

背包是啥

先介绍基础的背包问题，01背包，完全背包和多重背包。

1. 01背包

问题：有 N 件物品和一个容量为 V 的背包。放入第 i 件物品耗费的费用是 C i ，得到的价值是 W i 。求解将哪些物品装入背包可使价值总和最大。

每种物品只有选或不选两种情况，所以如果是暴力法时间复杂度也就是2^N，使用动态规划可以缩短至N * V。f[i][j]定义为前i个物品装入容量为j的背包的最大价值，f[i][j] = max(f[i - 1][j], f[i - 1][j - C[i]] + W[i])。

1
2
3
4
5
6

for (int i = 1; i <= N; i++) {
  	for (int j = C[i]; j <= V; j++) {
        if (j < C[i]) f[i][j] = f[i - 1][j];
      	else f[i][j] = Math.max(f[i - 1][j], f[i - 1][j - C[i]] + W[i]);
    }
}

可以降维，但是 j 需要倒序循环，是为了不影响 j 之后的位置的计算。因为f[j] 的计算实际要用到 f[i-1][j] 和 f[i-1][j-C[i]]，就是上一次循环的f[j] 和 f[j-C[i]]，如果是正序f[j-C[i]] 在本次循环中就已经被改变了。

1
2
3
4
5

for (int i = 1; i <= N; i++) {
		for (int j = V; j >= C[i]; j--) {
        f[j] = Math.max(f[j], f[j - C[i]] + W[i]);
    }		
}

有很多DP可以转为这样的01背包问题，比如416题，可以转化为找到数组中是否存在和为target的子序列。

2. 完全背包

问题：有 N 种物品和一个容量为 V 的背包，每种物品都有无限件可用。放入第 i 种物品的费用是 C i ，价值是 W i 。求解：将哪些物品装入背包，可使这些物品的耗费的费用总 和不超过背包容量，且价值总和最大。

每种物品虽然是无限个，但不是就有无限种情况，因为有容量的限制，所以每个物品的情况有k种，满足k * Ci < V，f[i][j]定义和之前相同，f[i][j] = max(f[i - 1][j - k*C[i]] + k*W[i])。其实可以把完全背包转化为01背包，即每个物品的多次选择看作对多个物品的01选择，比如 i物品最多只能选择7个，那么可以看作有7个 i 物品，然后对其进行01选择：

1
2
3
4
5
6
7

for (int i = 1; i <= N; i++) {
  	for (int j = 0; j <= V; j++) {
      	for (int k = 0; k * C[i] <= j; k++) {
          	f[i][j] = Math.max(f[i][j], f[i - 1][j - k * C[i]] + k * W[i]);
        }
    }
}

完全背包有三重循环，但可以将其优化为二重循环，完全背包的特点恰是每种物品可选无限件，所以在考虑加选一件第 i 种物品这种策略时， 正需要一个可能已选入第 i 种物品的子结果f[i][j - C[i]]。所以状态转移方程可以转化为f[i][j] = max(f[i - 1][j], f[i][j - C[i]] + W[i])：

1
2
3
4
5
6

for (int i = 1; i <= N; i++) {
  	for (int j = 1; j <= V; j++) {
      	if (j < C[i]) f[i][j] = f[i - 1][j];
      	else f[i][j] = Math.max(f[i - 1][j], f[i][j - C[i]] + W[i]);  //这里使用f[i - 1][j]是因为需要不使用第i个物品的解，而 f[i][j - C[i]] 是包含了从 1 到 V / C[i] 这些情况，都使用了第 i 个物品。
    }
}

最后这个方程同样也可以降维。这里不改变 j 的遍历顺序，因为 01 背包中每次比较的都是上一轮的值，而完全背包中比较的一个是上一轮的，一个是本轮的：

1
2
3
4
5

for (int i = 1; i <= N; i++) {
  	for (int j = C[i]; j <= V; j++) {
      	f[j] = Math.max(f[j], f[j - C[i]] + W[i]);
    }
}

322题凑硬币就是很经典的完全背包问题。377也是，但是包含了组合的知识。

发生了甚么

做项目时在构建函数调用图时明明把所有的结点和边信息都写入图中了，但在Echarts生成的图中结点间并没有边。

构建的图使用到了4个类：

1. classInfo 结点信息类、
2. clsasNode 结点类，包含classInfo类
3. classEdge 边类，包含了两个classNode类
4. classGraph 图类，包含了所有结点类和边类

原来是这样

原因是将图片转为echarts所需要的json格式时使用了HashMap遍历添加了图中所有结点，之后在把结点和边信息存为json时使用了HashMap中的containsKey方法，containsKey方法中使用了equals和hashCode方法，没有重写这两个方法导致了containsKey在判断时认为两个值相等的不同对象并不相等。

用上面的图举例子就是：

1. 声明一个 HashMap<classEdge, Integer> map
2. 声明一个classEdge变量edge1 = new classEdge(classNode1, classNode2) ，并添加进map中 map.put(edge1, 1)
3. 使用map.containsKey(new classEdge(classNode1, classNode2)) 时结果为false，因为虽然边的两个node是相同的，但是因为没有重写equals和hashCode方法，这两个边被认为是不同的

我啪的一下解决了，很快啊

解决方法就是每个类中都重写了hashCode和equals方法。在Idea里可以自动生成这两个方法，超方便。

那为什么重写equals方法也必须重写hashCode呢，首先有下面的规定：

1. 如果两个对象通过equals方法比较是相等的，那么要求这两个对象的hashCode方法返回的值也应该是相等的。
2. 如果两个对象通过equals方法比较是不同的，那么也不要求这两个对象的hashCode方法返回的值是不相同的。但是我们应该知道对于不同对象产生不同的哈希值对于哈希表(HashMap等等)能够提高性能。

所以如果不重写hashcode方法，那么两个不同的对象equals时，hash值却不同，如果把对象用在map中作为键使用时就会出现上面的错误。

DP主要用来解决两类问题：计数，优化。计数是说给一些资源，去得到某种解的方法数有多少或者得到某种解的最（大/小）值。优化是说很多时间复杂度达到2^n的搜索、递归问题可以用DP来优化。

使用DP有三个要求：最优子结构（把大问题分为多个小问题，只要最优解决小问题就可以最优解决大问题），子问题被重复求解（overlapped，重复了才能优化嘛），没有后效性（子问题的最优解不会在解决后面的较大问题时被改变）。

获得状态转移方程是最难的一步，总结了一点点思路

1. 遍历以求得的所有解

得到某一种状态需要遍历前面所有已经得出的状态，即求 f[i] 需要遍历 f[1], f[2], …, f[i - 1]。139，813，312，300，410都是这样。

还有312题戳破气球f[i][j]需要遍历 f[i][k] 和 f[k][j] 两个状态。

139、单词拆分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

public boolean wordBreak(String s, List<String> wordDict) {
    // f[i] 从第1个到第i个字符的子字符串能否被拆分
    // f[i] = (f[1]...f[k] && dict.contains(s.substring(k, i)))   k >= 0 && k < i
    // 时间复杂度：O(n^2)  空间复杂度：O(n)

    HashSet<String> dict = new HashSet<>();
    for (String str : wordDict) {
      dict.add(str);
    }
    boolean[] f = new boolean[s.length() + 1];
    f[0] = true;
    for (int i = 1; i <= s.length(); i++) {
      for (int k = 0; k < i; k++) {				//这里遍历所有可能解
        if (f[k] && dict.contains(s.substring(k, i))) {
          f[i] = true;
          break;
        }
      }
    }
    return f[s.length()];
}

873题一维数组无法表示状态，也需要二维来记录所有以i，j结尾的子序列的长度，并利用HashMap来进行记忆

2. 状态机

在某一个时刻或位置会有几种不同的状态，不同状态间的转换有一些限制，用这些限制就可以写出状态转移方程。比如309、801题

309、存在冷却期的股票买卖

在卖出后必须冷却一天才能继续买入，每天只能干三件事，买入、啥也不干、卖出。那么状态可以直接设为这3种情况吗？

实际上不行，因为这里啥也不干包括了2种情况：手里持股啥也不干和不持股啥也不干。那分为四个状态呢？就可以进行计算了。这里还可以降维：

1
2
3
4

f[i][0]  买入。     = f[i - 1][2] - A[i]
f[i][1]  持股啥也不干   = max(f[i - 1][0], f[i - 1][1])
f[i][2]  不持股啥也不干 = max(f[i - 1][2], f[i - 1][3])
f[i][3]  卖出。     = max(f[i - 1][0], f[i - 1][1]) + A[i]

不过前两种状态实际上也可以合并为一个状态，那就是存在3种状态，持有、休息、卖出：

1
2
3

f[i][0]  到第i天持有     = max(f[i - 1][0], f[i - 1][1] - prices[i])
f[i][1]  到第i天休息状态  = max(f[i - 1][1], f[i - 1][2])
f[i][2]  到第i天售出状态  = f[i - 1][0] + prices[i]

（72题编辑距离中每一步有四种操作方式达到，这状态转移也是有点类似的哦）

3. 问题转化

比如576题，将(i, j) 位置上的球移出界的路径数可以转化为将界外的球移到 (i, j) 位置的路径数；

416分割等和子集的题可以转为求和为是否存在和为 sum 一半的子序列

4. 关于矩阵的

1. 通过dp[i][j] = dp[i][j - 1] + dp[i - 1][j] - dp[i - 1][j - 1] + mat[i -1][j -1];先计算出所有左上角到 (i, j) 点的矩形区域的和
2. 然后可以快速得到任意指定矩形区域的和，区域 (x1, y1) 到 (x2, y2) 的和为 dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1];

比如1292，1314题，在 n^2 时间内就可以得到所有区域的和了，否则时间复杂度将达到 n^4

5. 空间压缩

很多题都可以进一步压缩空间复杂度，这种题大多数状态转移方程只需要用到前一层或后一层状态，所以可能需要一个额外的一维数组或者变量进行记录，比如121，416题等。322零钱兑换也是不错的。

121: f[i] = max(f[i - 1], A[i] - l[i]) l[i] 表示前i天的最低价。 >>>> res = max(res, A[i] - lowest) 用lowest代替 L 数组

416: f[i][j] = f[i - 1][j] || f[i - 1][j - A[i]] >>>> f[j] = f[j] || f[j - A[i]]

f[i][j] = f[i - 1][j] >>>> memo = f; memo[j] = f[j]; f = memo 声明一个memo数组，最后再全部赋值给f

f[i][j] = f[i + 1][j - 1] 这个i由i+1得到，所以要倒序遍历i >>>> f[i] = max(f[i], f[i - 1]) ，但要记录前一个值，详细看下面516题

516、最长回文字子串题就可以用到滚动数组进行压缩，滚动数组还可以进一步压缩为一个临时变量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

public int longestPalindromeSubseq(String s) {
  // f[i][j]   从第i个字符到第j个字符是否是回文字
  // f[i][j] = f[i + 1][j - 1]  if (s[i] == s[j])

  // 滚动数组
  int[] f0 = new int[s.length() + 1];   //状态压缩，f0[i]表示长度为l - 1的到第i个字符为止的字符串

  if (s.equals("")) return 0;

  for (int i = 1; i <= s.length(); i++) f0[i] = 1;
  
  for (int i = s.length(); i >= 1; i--) {
    int pre = 0;
    for (int j = i + 1; j <= s.length(); j++) {
      int temp = f0[j];
      if (s.charAt(i - 1) == s.charAt(j - 1)) {
        f0[j] = pre + 2;
      } else f0[j] = Math.max(f0[j], f0[j - 1]);
      pre = temp;
    }
  }
  return f0[s.length()];
}

486题赢家预测，状态转移方程是f[i][j] = Math.max(nums[i - 1] - f[i + 1][j], nums[j - 1] - f[i][j - 1]); f[i][j]表示第i到j元素的先手比后手赢的最多分数，这种写法没法降维了。不过把f[i][j]改为长度为 i，开始元素是j的子序列中先手比后手多的分数的话就可以降维了，max(nums[j] - f[i - 1][j + 1], nums[j + i - 1] - f[i - 1][j]); >>>> f[j] = max(nums[j] - f[j + 1], nums[j + i - 1] - f[j])

6. Other

还有些题连状态方程都很难想，比如486猜赢家，f[i][j]表示从i到j的子序列，先手和后手的分差。啊凭经验与运气了。

有时还需要一个HashMap记录之前的状态来快速获取结果，如823，873。

那就先写这么多，之后有新的想法再更新，那我现在走吧。我是郭富城！

主要有下面几个问题，怎样判断哪些对象可以被回收？怎样回收？方法区的常量和类怎样回收？，基本是深入理解Java虚拟机书中的内容。

怎样判断哪些是可回收的垃圾呢？

两种方法：

1. 引用计数法：每次引用对象都会在该对象的引用计数器上加一，引用失效时就减一，计数为0时就可被回收，但是这种方法可能出现循环引用，就是ab两个对象相互引用

2. 可达性分析：通过GC roots对象为起点向下搜索，和被引用的对象间存在引用链，如果一个对象到GCroots没有任何引用链，就可被回收。GCroots对象一般包括：

   1. 虚拟机栈中引用的对象
   2. 方法区中类静态属性引用的对象
   3. 方法区中常量引用的对象
   4. 本地方法栈中JNI引用的对象

但是也不是说只要有引用存在就一定不会被回收，这种说法是针对强引用而言的。如果是软引用、弱引用、虚引用的对象，即使该对象还被引用着，也可能会被回收。

记录学习redis的一点基础东西

基础

介绍

Redis是一个开源的高性能的key-value存储系统，主要解决海量数据和高并发需求。具有以下特点：

1. Redis是非关系型（NoSQL）数据库。本质上也是数据库，但MySQL关系型数据库存储时必须定义数据词典，而Redis则不需要，它是作为关系型数据库的补充。
2. Redis是**基于内存**的，所以比基于硬盘的MySQL要快很多，但非常吃内存
3. Redis支持数据的持久化，可以将内存中的数据保持在磁盘中，重启的时候可以再次加载进行使用。
4. Redis提供String，list，set，sorted set，hash等数据结构的存储。
5. Redis支持数据的备份，即master-slave模式的数据备份。
6. 内部采用单线程机制工作。
7. Redis是远程的，有客户端和服务端，我们一般说的是服务端。

Redis优势：

1、性能极高 – Redis能读的速度是110000次/s,写的速度是81000次/s 。
2、丰富的数据类型 – Redis支持二进制案例的 String, List, Hash, Set 及 Sorted Set 数据类型操作。
3、原子 – Redis的所有操作都是原子性的，同时Redis还支持对几个操作全并后的原子性执行。
4、丰富的特性 – Redis还支持 publish/subscribe, 通知, key 过期等等特性

8.用通配符进行过滤

通配符本身实际是SQL的WHERE子句中有特殊含义的字符

为在搜索子句中使用通配符，必须使用LIKE操作符。LIKE指示MySQL，后跟的搜索模式利用通配符匹配而不是直接相等匹配进行比较

最常使用的通配符是百分号（%）。在搜索串中，%表示任何字符出现任意次数。

where prod_name LIKE 'jet%';

下划线（_）。下划线的用途与%一样，但下划线只匹配单个字符而不是多个字符

通配符搜索的处理一般要比前面讨论的其他搜索所花时间更长

9.用正则表达式进行搜索

正则表达式是用来匹配文本的特殊的串（字符集合）

where prod_name REGEXP 'xxx';

10.创建计算字段

直接从数据库中检索出转换、计算或格式化过的数据；而不是检索出数据，然后再在客户机应用程序或报告程序中重新格式化

使用Concat()函数来拼接两个列，例：Concat(vend_name, '(', vend_country, ')');

还可以执行算术计算

11.使用数据处理函数

文本处理函数：

• Left() 返回串左边的字符
• Length() 返回串的长度
• Locate() 找出串的一个子串
• Lower() 将串转换为小写
• LTrim() 去掉串左边的空格
• Right() 返回串右边的字符

CSAPP中链接的一点总结

• 链接器操作的目标文件（可重定位）
  • ELF可重定位目标文件格式
  • 符号和符号表
• 链接器开始工作了
  • 符号解析
  • 重定位
• 可执行目标文件是什么
  • ELF可执行目标文件格式
  • 如何加载可执行目标文件
• 链接库
  • 编译时加载静态库
  • 运行时加载动态库

目标文件

源代码在经过预处理，编译，汇编等操作后生成可重定位目标文件，可重定向文件再通过链接器生成可执行目标文件。可重定位目标文件通过名字可知文件中的一些符号之后需要在内存中重定向。

掌握链接有助于理解分离编译的过程，作用域的实现以及如何利用共享库等。

在不同阶段生成的目标文件可分为三种，之后再每个详细说明：

• 可重定位目标文件
• 可执行目标文件
• 共享目标文件

逻辑流：pc值的序列叫逻辑控制流，简称逻辑流

并发：多个逻辑流执行时相互重叠，称为并发流，这种现象叫做并发（concurrency）

并行：并行流是并发流的真子集，两个流并发运行在不用的核或计算机上称为并行流

应用程序实现并发的三种方法

进程

每个逻辑控制流都是一个进程，有其独立的虚拟地址空间

• 服务器在收到客户端请求后生成子进程单独处理，处理完后要回收僵尸进程
• 不同进程间不共享数据，所以需要用IPC进行进程间通讯
• 父进程和子进程都有 listenfd 和 connfd，所以在父进程中需要关闭 connfd，在子进程中需要关闭 listenfd

优点：独立的地址空间使一个进程不会覆盖别的进程的虚拟存储器

缺点：1. 共享信息更困难；2. 依靠IPC开销较高，会比较慢